Ever wondered how movies and games manage to animate the world so well?
Well, I have but it’s probably not with ray tracing…
What is ray tracing?
Ray tracing is a technique to render physical objects (e.g. a sphere) to an image. It simulates rays of light and their interactions with objects. It can produce some pretty good looking images, almost indistinguishable from a real photograph:

I wanted to try this out for myself, so I began implementing it in c++, the code is on github.
Imagine a ball on a flat surface and a camera looking at it as in the figure below. In the real world, light is emitted from the light source and is scattered in every direction. Some of the light makes it to the ball and scatters again in all directions. A portion of that light scatters in the direction of our camera and is detected.
We only concern ourselves with the rays that hit the camera, because those are the ones we actually see. So instead of trying to calculate all the light and see what part of it makes it to the camera, we follow the light path from the other direction.

Pixels
An image consists of a grid of square pixels. For each pixel we trace a line from the camera through the pixel, much like the red lines in the figure. If it hits an object, we check if the point of impact is being lit by the light source. For example, two of the red lines (rays) hit the ball in an illuminated spot, but the third ray hits the floor in a place where the path to the light source is blocked by the ball.
After implementing the math (see below), the previous scene is recreated by placing a sphere on a surface and putting a light on the left side above the ball:

Shader
Although we can simulate shadows cast by objects, it still looks ugly because the amount of light that is bouncing of the ball is the same everywhere. In reality however, the intensity depends on the the angle of the surface you are looking at.
For example, a piece of ball surface is more lit when its surface faces the light source, compared to a piece of ball surface which faces away from the light source. This is because the same amount of light rays hit a larger area of the ball when the surface is at a large angle.
When this is taken into account, the resulting image looks much more like an actual scene, altough very dark with only a single light source.

Let’s create another scene with multiple light sources and objects to test if everything is implemented correctly.

By changing the position of the viewpoint (camera), the still scene comes alive a bit.
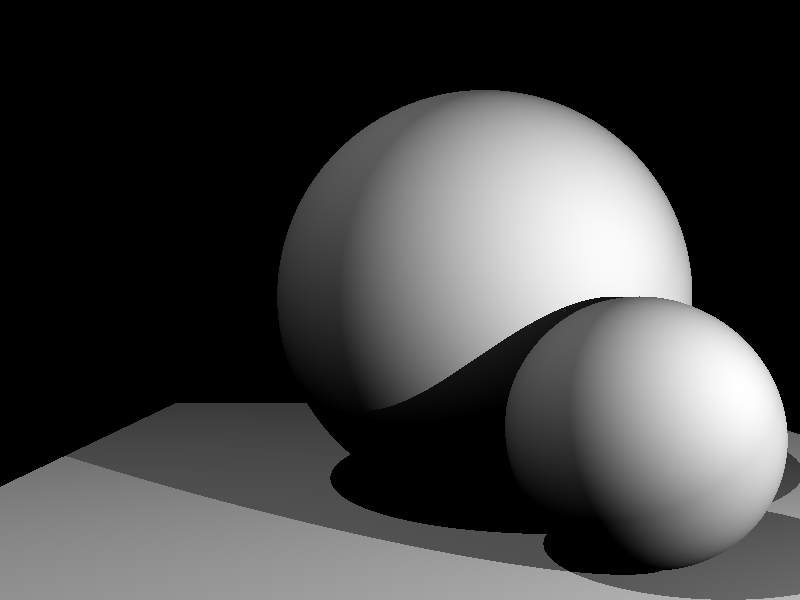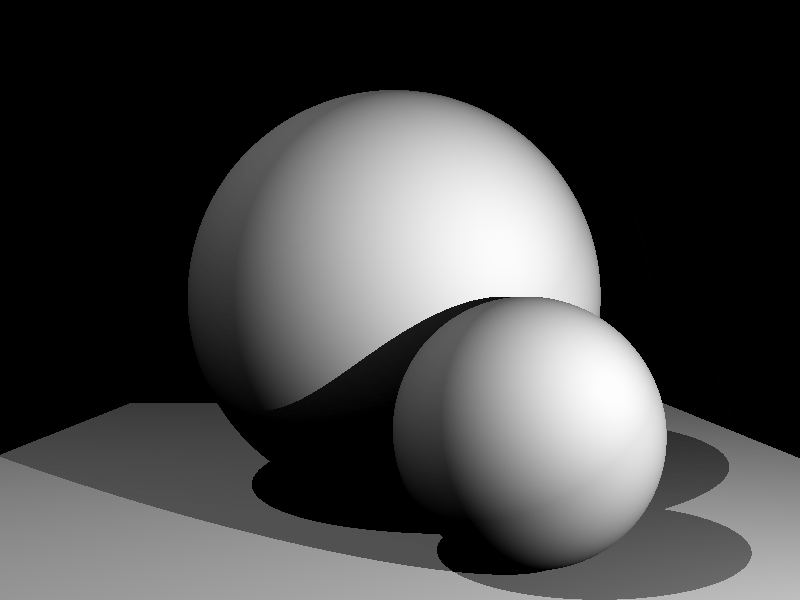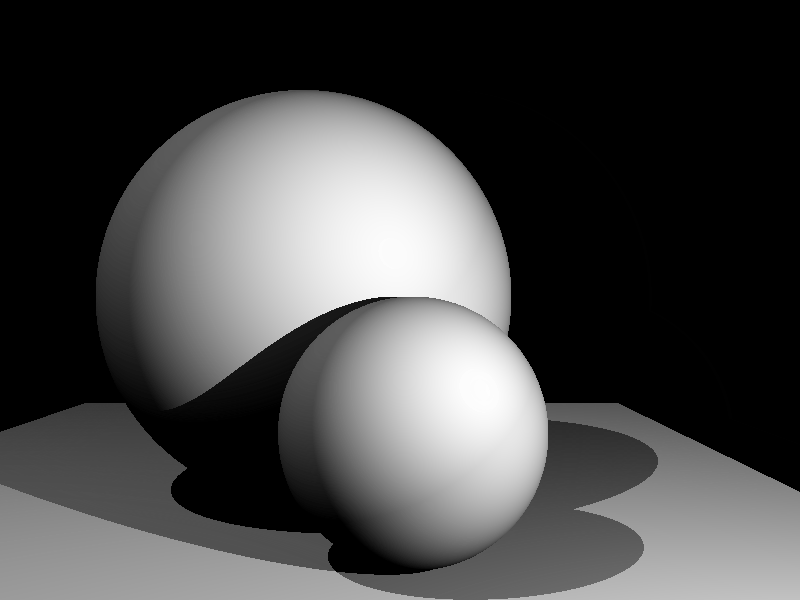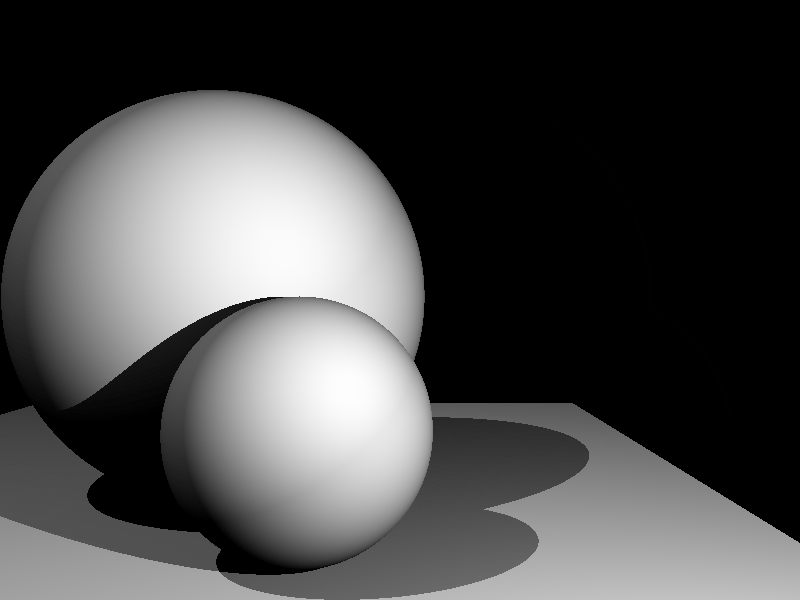
Math
The Math behind ray tracing spheres and planes is suprisingly simple! In order to implement this, you only need two ingredients:
- Intersection of ray with an object
- Lambertian reflectance
Ray-object intersection
On multiple occasions we need to calculate the intersection of a line with an object. Only the sphere is considered, see the figure below:
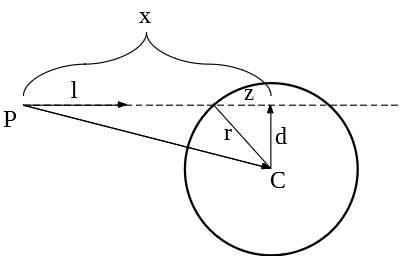
First, project the vector to the sphere center (\vec{PC}) onto the actual ray \vec{l} with \vec{x} = \hat{l} \cdot \left( \vec{PC} \cdot \hat{l} \right) .
Then, calculate the difference \vec{d} with \vec{d} = \vec{x} – \vec{PC} . Notice that this is a right angle and its length can be used to check if the line actually intersects with the sphere:
If |\vec{d}| > r , the line does not intersect the sphere and should be ignored.
Otherwise, calculate the position of the intersection. This can be done by first calculating z = \sqrt{ r^2-|\vec{d}|^2 }. With that, the location of impact from point \vec{P} is: (|\vec{x}|-z) \hat{l}
The other intersection can be ignored for now because the ball is a solid object and we only care about diffuse reflection.
How to calculate intersections with a flat surface is left as an exercise to the reader.
Lambertian reflectance
Most of the light that you see reflected of an object is diffusive, which means that a surface reflects incoming light to all directions. Lambertian reflectance is a good way to model this kind of reflection.
Suppose we know where a light ray hits an object, the amount of light that is diffused is proportional to the angle between the light ray and the surface normal. Given a light source intensity of I and a diffusion coefficient \mu , the total light diffused is:
I \cdot \mu \cdot \max(0, \hat{n}\cdot\hat{l})where \hat{n} is the normal of the object surface at impact and \hat{l} is vector from impact to the light.
What next?
The power of ray tracing lies with reflections. For traditional rendering techniques, reflections need to be artifically put in with a lot of effort. With ray tracing, reflections emerge naturally if you consider more bounces for each ray. Here, I only considered if a piece of surface was illuminated by a light source or not and how much light is reflected. The next step would be to consider the path of light that bounces of two objects before hitting the camera, but I’ll do that another time.
Maybe…
